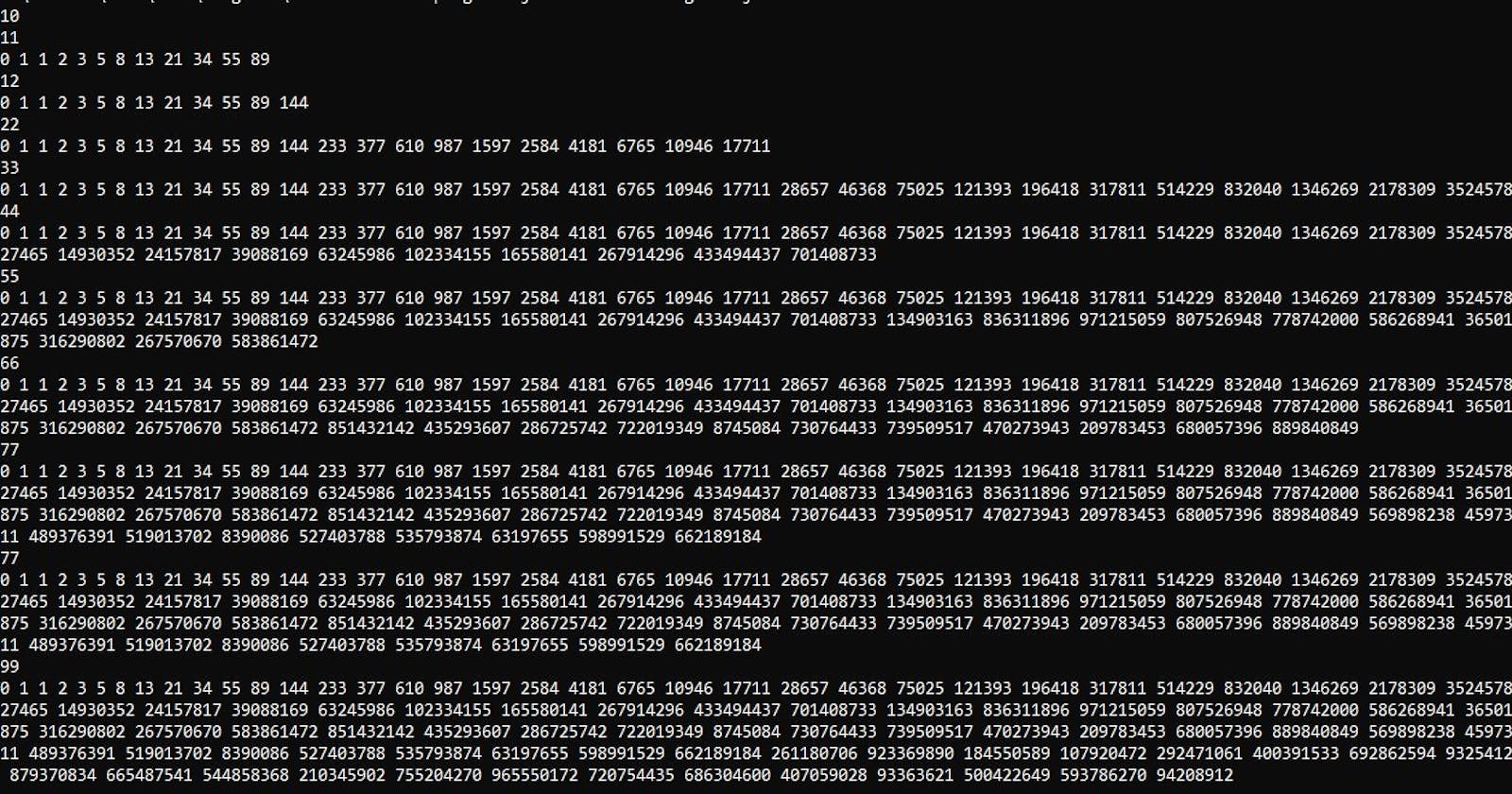
Fibonacci Series using Modulo Arithmetic - Java

Fibonacci series using modulo arithmetic:

An array res is initialized to store the Fibonacci numbers, with size n + 1 to include n numbers.

int M = 1000000007;: The variable M is set to the modulo value ( 10^9 + 7 ).

res[0] = 0; res[1] = 1;: The first two Fibonacci numbers, 0 and 1, are directly assigned to res.

for(int i = 2; i <= n; i++) { res[i] = (res[i - 2] + res[i - 1]) % M; }: Using a loop starting from index 2, each Fibonacci number is calculated as the sum of the previous two numbers in res, modulo M.

Finally, the array res containing Fibonacci numbers up to index n is returned.

This implementation is efficient for generating Fibonacci numbers up to large values of ( n ) while handling integer overflow by using modular arithmetic.

//Driver Code Starts
import java.io.*;
import java.util.*;

class Main {
    // Driver code
    public static void main(String[] args) throws Exception {
        BufferedReader br =
            new BufferedReader(new InputStreamReader(System.in));
        int t = Integer.parseInt(br.readLine().trim());
        while (t-- > 0) {
            int n = Integer.parseInt(br.readLine().trim());
            Solution obj = new Solution();
            int ans[] = obj.Series(n);
            for (int i : ans) {
                System.out.print(i + " ");
            }
            System.out.println();
        }
    }
}//Driver Code Ends

class Solution {

    int[] Series(int n) {
        // code here
        int[] res=new int[n+1];
    int M=1000000007;
    res[0]=0;
    res[1]=1;
    for(int i=2;i<=n;i++)
    {
     res[i]=(res[i-2]+res[i-1]) % M;   
    }
    return(res);
    }
}

Thanks for reading.